Día de la ciencia del "Colegio Diocesano San Jose" Tema Brazo Mecanico 7-A
Un brazo hidráulico es una estructura o aparato mecánico que se divide en tres partes unidas entre si y que se pueden mover independiente mente una de la otra y dichos movimientos son realizados por aumento o disminución de la presión ejercida por un medio liquido y un medio gaseoso, su nombre se deriva porque es parecido a un brazo donde las tres partes serian la mano con sus dedos, el brazo y el antebrazo y las partes donde se unen serian la muñeca y el codo, ahora hidráulico es porque como ya te dije que los movimientos son por medio de presión de un liquido que es su caso es aceite mecánico y un gas que están bajo presión, entonces si unimos los términos nos queda Brazo Hidráulico.
Al aumentar la presión el brazo se extiende y al disminuir la presión el brazo se destiende o recoge, el brazo hidráulico más común es la pieza que tienen atrás muchas palas mecánicas y la cual le permite sacar material formando una zanja, si la has visto alguna vez sabes cual es.
Las Excabadoras Utilizan un Brazo Hidráulico O Mecanico para Recojer Tierra del Suelo Con las Facilidad
El principio de Pascal puede ser interpretado como una consecuencia de la ecuación fundamental de la hidrostática y del carácter altamente incompresible de los líquidos. En esta clase de fluidos la densidad es prácticamente constante, de modo que de acuerdo con la ecuación:
Donde:
 , presión total a la profundidad.
, presión total a la profundidad. , presión sobre la superficie libre del fluido.
, presión sobre la superficie libre del fluido. , densidad del fluido.
, densidad del fluido. , aceleración de la gravedad.
, aceleración de la gravedad. , Altura, medida en Metros.
, Altura, medida en Metros.
La presión se define como la fuerza ejercida sobre unidad de área p = F/A. De este modo obtenemos la ecuación: F1/A1 = F2/A2, entendiéndose a F1 como la fuerza en el primer pistón y A1 como el área de este último. Realizando despejes sobre esta ecuación básica podemos obtener los resultados deseados en la resolución de un problema de física de este orden.
Si se aumenta la presión sobre la superficie libre, por ejemplo, la presión total en el fondo ha de aumentar en la misma medida, ya que el término ρgh no varía al no hacerlo la presión total. Si el fluido no fuera incompresible, su densidad respondería a los cambios de presión y el principio de Pascal no podría cumplirse. Por otra parte, si las paredes del recipiente no fuesen indeformables, las variaciones en la presión en el seno del líquido no podrían transmitirse siguiendo este principio.
Prensa hidráulica
La prensa hidráulica es una máquina compleja que permite amplificar la intensidad de las fuerzas y constituye el fundamento deelevadores, prensas, frenos y muchos otros dispositivos hidráulicos de maquinaria industrial.
La prensa hidráulica constituye la aplicación fundamental del principio de Pascal y también un dispositivo que permite entender mejor su significado. Consiste, en esencia, en dos cilindros de diferente sección comunicados entre sí, y cuyo interior está completamente lleno de un líquido que puede ser agua o aceite. Dos émbolos de secciones diferentes se ajustan, respectivamente, en cada uno de los dos cilindros, de modo que estén en contacto con el líquido. Cuando sobre el émbolo de menor sección S1 se ejerce una fuerza F1 la presión p1 que se origina en el líquido en contacto con él se transmite íntegramente y de forma casi instantánea a todo el resto del líquido. Por el principio de Pascal esta presión será igual a la presión p2 que ejerce el fluido en la sección S2, es decir:
con lo que las fuerzas serán, siendo, S1 < S2 :
y por tanto, la relación entre la fuerza resultante en el émbolo grande cuando se aplica una fuerza menor en el émbolo pequeño será tanto mayor cuanto mayor sea la relación entre las secciones:
Discusión teórica
En un fluido las tensiones compresivas o presiones en el mismo pueden representarse mediante un tensor de la forma:
(1)
Eso significa que fijado un punto  en el seno del fluido y considerando una dirección paralela al vector unitario
en el seno del fluido y considerando una dirección paralela al vector unitario 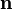 la fuerza por unidad de área ejercida en ese puntos según esa dirección o el vector tensión
la fuerza por unidad de área ejercida en ese puntos según esa dirección o el vector tensión 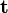 viene dado por:
viene dado por:
 en el seno del fluido y considerando una dirección paralela al vector unitario
en el seno del fluido y considerando una dirección paralela al vector unitario 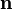 la fuerza por unidad de área ejercida en ese puntos según esa dirección o el vector tensión
la fuerza por unidad de área ejercida en ese puntos según esa dirección o el vector tensión 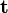 viene dado por:
viene dado por:(2)
El principio de Pascal establece que la tensión en () es independiente de la dirección 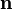 , lo cual sólo sucede si el tensor tensión es de la forma:2
, lo cual sólo sucede si el tensor tensión es de la forma:2
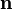 , lo cual sólo sucede si el tensor tensión es de la forma:2
, lo cual sólo sucede si el tensor tensión es de la forma:2(3)
Donde p es una constante que podemos identificar con la presión. A su vez esa forma del tensor sólo es posible tenerlo de forma aproximada si el fluido está sometido a presiones mucho mayores que la diferencia de energía potencial entre diferentes partes del mismo. Por lo que el principio de Pascal puede formularse como: «En un fluido en reposo y donde las diferencias de altura son despreciables el tensor de tensiones del fluido toma la forma dada en ()».
Sin embargo, en realidad debido al peso del fluido hace que el fluido situado en la parte baja de un recipiente tenga una tensión ligeramente mayor que el fluido situado en la parte superior. De hecho si la única fuerza másica actuante es el peso del fluido, el estado tensional del fluido a una profundidad z el tensor tensión del fluido es:
(4)
En vista de lo anterior podemos afirmar que «fijado un punto de un fluido incompresible en reposo y contenido en un recipiente bajo presión e indeformable, la presión del fluido, es idéntica en todas direcciones, y su tensor tensión viene dado por


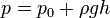

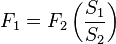



No hay comentarios:
Publicar un comentario